Equações com sen x = a

Equações trigonométricas são igualdades que evolvem uma ou mais funções trigonométricas de arcos incógnitos. Para a resolução de equações trigonométricas não existe um processo único, o que devemos fazer é tentar reduzi-las a equações mais simples, do tipo senx = α,
cosx = α e tgx = α, denominadas equações fundamentais. Das três equações citadas vamos abordar os conceitos e as formas de resolução da equação senx = α.

As equações trigonométricas na forma senx = α possui soluções no intervalo –1 ≤ x ≤ 1. A determinação dos valores de x que satisfazem esse tipo de equação obedecerá à seguinte propriedade: Se dois arcos têm senos iguais, então eles são côngruos ou suplementares.

Consideremos x = α uma solução da equação sen x = α. As outras possíveis soluções são os arcos côngruos ao arco α ou ao arco π – α. Então: sen x = sen α. Observe a representação no ciclo trigonométrico:

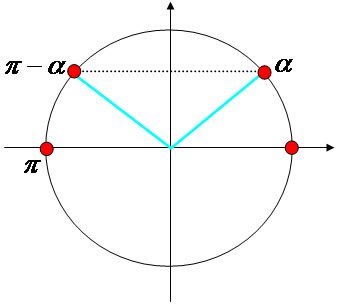
Concluímos que:
x = α + 2kπ, com k Є Z ou x = π – α + 2kπ, com k Є Z

Exemplo

Resolva a equação: sen x = √3/2

Sabemos pela tabela de razões trigonométricas que √3/2 corresponde ao seno do ângulo de 60º. Então:
sen x = √3/2 → sen x = π/3 (π/3 = 180º/3 = 60º)

Dessa forma, a equação senx = √3/2 possui como solução todos os arcos côngruos ao arco π/3 ou ao arco π – π/3. Observe ilustração:

Concluímos que as possíveis soluções da equação sen x = √3/2 são:
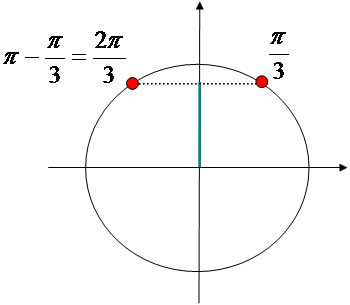
x = π/3 + 2kπ, com k Є Z ou x = 2π/3 + 2kπ, com k Є Z


C*