Equações com cos x = a

As equações trigonométricas são igualdades que envolvem funções trigonométricas de arcos desconhecidos. A resolução dessas equações consiste num processo único, que utiliza técnicas de redução a equações mais simples. Vamos abordar os conceitos e as definições das equações na forma cosx = a.

As equações trigonométricas na forma cosx = α possui soluções no intervalo –1 ≤ x ≤ 1. A determinação dos valores de x que satisfazem esse tipo de equação obedecerá à seguinte propriedade: Se dois arcos têm cossenos iguais, então eles são côngruos ou replementares.

Consideremos x = α uma solução da equação cos x = α. As outras possíveis soluções são os arcos côngruos ao arco α ou ao arco – α (ou ao arco 2π – α) . Então: cos x = cos α. Observe a representação no ciclo trigonométrico:

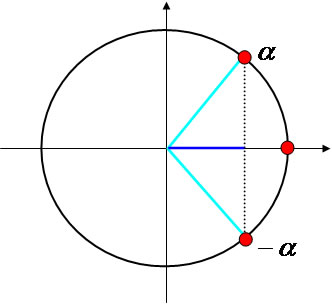
Concluímos que:
x = α + 2kπ, com k Є Z ou x = – α + 2kπ, com k Є Z


Exemplo 1

Resolver a equação: cos x = √2/2.

Pela tabela de razões trigonométricas temos que √2/2 corresponde ao ângulo de 45º. Então:

cos x = √2/2 → cos x = π/4 (π/4 = 180º/4 = 45º)

Dessa forma, a equação cosx = √2/2 possui como solução todos os arcos côngruos ao arco π/4 ou –π/4 ou ainda 2π – π/4 = 7π/4. Observe ilustração:

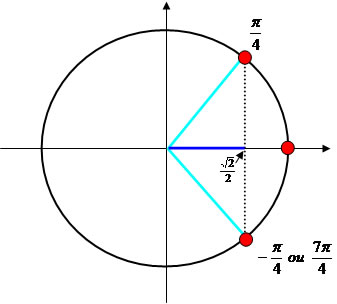
Concluímos que as possíveis soluções da equação cos x = √2/2 são:
x = π/4 + 2kπ, com k Є Z ou x = – π/4 + 2kπ, com k Є Z

Exemplo 2

Resolver a equação: cos 3x = cos x

Quando os arcos 3x e x são côngruos:
3x = x + 2kπ
3x – x = 2kπ
2x = 2kπ
x = kπ

Quando os arcos 3x e x são replementares:
3x = –x + 2kπ
3x + x = 2kπ
4x = 2kπ
x = 2kπ/4
x = kπ/2

A solução da equação cos 3x = cos x é {x Є R / x = kπ ou x = kπ/2, com k Є Z}.

C*