Comprimento de um arco

Dada uma circunferência de centro O, raio r e dois pontos A e B pertencentes à circunferência, temos que a distância entre os pontos assinalados é um arco de circunferência. O comprimento de um arco é proporcional à medida do ângulo central, quanto maior o ângulo, maior o comprimento do arco; e quanto menor o ângulo, menor o comprimento do arco.

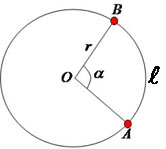
Para determinarmos o comprimento de uma circunferência utilizamos a seguinte expressão matemática: C = 2*π*r. A volta completa em uma circunferência é representada por 360º. Vamos realizar uma comparação entre o comprimento da circunferência em medida linear (ℓ) e medida angular (α), observe:

linear	angular
2*π*r	360º
ℓ	α

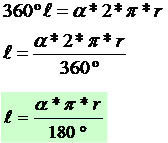
Essa expressão pode ser utilizada para determinar o comprimento do arco de uma circunferência de raio r e ângulo central α em graus. Nesses casos utilize π = 3,14.

Caso o ângulo central seja dado em radianos, utilizamos a seguinte expressão: ℓ = α * r.

Exemplo 1

Determine o comprimento de um arco com ângulo central igual a 30º contido numa circunferência de raio 2 cm.

ℓ = α * π * r / 180º
ℓ = 30º * 3,14 * 2 / 180º
ℓ = 188,40 / 180
ℓ = 1,05 cm

O comprimento do arco será de 1,05 centímetros.


Exemplo 2

O ponteiro dos minutos de um relógio de parede mede 10 cm. Qual será o espaço percorrido pelo ponteiro após 30 minutos?

Veja a figura do relógio:

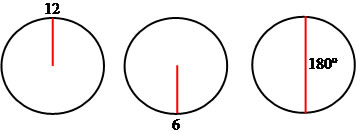
ℓ = α * π * r / 180º
ℓ = 180º * 3,14 * 10 / 180º
ℓ = 5652 / 180
ℓ = 31,4 cm

O espaço percorrido pelo ponteiro dos minutos será de 31,4 centímetros.


Exemplo 3

Determine o comprimento de um arco com ângulo central medindo π/3 contido numa circunferência de 5 cm de raio.

ℓ = α * r
ℓ = π/3 * 5
ℓ = 5π/3
ℓ = 5*3,14 / 3
ℓ = 15,7 / 3
ℓ = 5,23 cm


Exemplo 4

Um pêndulo de 15 cm de comprimento oscila entre A e B descrevendo um ângulo de 15º. Qual é o comprimento da trajetória descrita pela sua extremidade entre A e B?

ℓ = α * π * r / 180º
ℓ = 15º * 3,14 * 15 / 180º
ℓ = 706,5 / 180
ℓ = 3,9 cm


C*