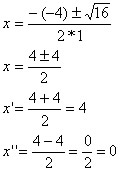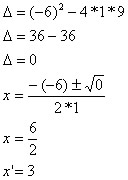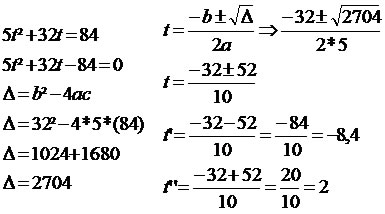Inequação modular

Uma inequação será identificada como modular se dentro do módulo tiver uma expressão com uma ou mais incógnitas, veja alguns exemplos de inequações modulares:

|x| > 5

|x| < 5

|x – 3| ≥ 2

Ao resolvermos uma inequação modular buscamos encontrar os possíveis valores que a incógnita deverá assumir, obedecendo às regras resolutivas de uma inequação e as condições de existência de um módulo.

Condição de existência de um módulo, considerando k um número real positivo:

Se |x| <> k então, x < – k ou x > k

Para compreender melhor a resolução de inequações modulares veja os exemplos abaixo:

Exemplo 1

|x| ≤ 6

Utilizando a seguinte definição: se |x| <>– 6 ≤ x ≤ 6

S = {x Є R / – 6 ≤ x ≤ 6}

Exemplo 2

|x – 7| <>

Utilizando a seguinte definição: se |x| <>– 2 <>

S = {x Є R / 5 < x e x < 9 }



Exemplo 3


|x² – 5x | > 6

Precisamos verificar as duas condições:

|x| > k então, x < – k ou x > k

|x| <>

Fazendo |x| > k então, x < – k ou x > k
x² – 5x > 6
x² – 5x – 6 > 0
Aplicando Bháskara temos:
x’ = 6
x” = –1

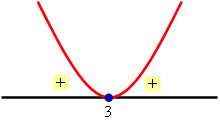
Pela propriedade:
x > 6
x < –1

Fazendo |x| < k então, – k < x < k x² – 5x < – 6 x² – 5x + 6 < 0 Aplicando Bháskara temos:
x’ = 3
x” = 2

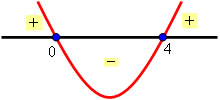
Pela propriedade:
x > 2
x < 3

S = {x Є R / x < –1 ou 2 <> 3 ou x>6}.


C*

Inequação do 2º grau

As inequações são expressões matemáticas que utilizam na sua formatação, os seguintes sinais de desigualdades:

>: maior que

<: menor que

≥: maior ou igual

≤: menor ou igual

≠: diferente

As inequações do 2º grau são resolvidas utilizando o teorema de Bháskara. O resultado deve ser comparado ao sinal da inequação, com o objetivo de formular o conjunto solução.

Exemplo 1

Vamos resolver a inequação 3x² + 10x + 7 <>.

S = {x Є R / –7/3 <>

Exemplo 2

Determine a solução da inequação –2x² – x + 1 ≤ 0.

S = {x Є R / x < –1 ou x > 1/2}



Exemplo 3

Determine a solução da inequação x² – 4x ≥ 0.

S = {x Є R / x ≤ 0 ou x ≥ 4}


Exemplo 4

Calcule a solução da inequação x² – 6x + 9 > 0.

S = {x Є R / x <3> 3} ou S = {x Є R / x ≠ 3 }

OBS: SEMPRE coloquem a solução do jeito mostrado.

c*

Função do 2º Grau - Exercicios

Exemplo 1

O movimento de um projétil, lançado para cima verticalmente, é descrito pela equação y = – 40x² + 200x. Onde y é a altura, em metros, atingida pelo projétil x segundos após o lançamento. A altura máxima atingida e o tempo que esse projétil permanece no ar correspondem, respectivamente, a:

Resolução:

Veja o gráfico do movimento:

Na expressão y = –40x² + 200x os coeficientes são a = –40, b = 200 e c = 0.

Utilizaremos a expressão Yv para obter a altura máxima atingida pelo objeto:

O objeto atingiu a altura máxima de 250 metros.


Utilizaremos a expressão Xv para obter o tempo de subida do objeto:

O projétil levou 2,5s para atingir altura máxima, levando mais 2,5s para retornar ao solo, pois no movimento vertical o tempo de subida é igual ao tempo de descida. Portanto, o projétil permaneceu por 5 s no ar.


Exemplo 2

Um objeto foi lançado do topo de um edifício de 84 m de altura, com velocidade inicial de 32 m/s. Quanto tempo ele levou para chegar ao chão? Utilize a expressão matemática do 2º grau d = 5t² + 32t, que representa o movimento de queda livre do corpo.

Resolução:

O corpo percorreu a distância de 84 m que corresponde à altura do edifício. Portanto, ao substituirmos d = 84, basta resolvermos a equação do 2º grau formada, determinando o valor do tempo t, que será a raiz da equação.

t = 2 segundos, pois para t=-8,4 é impossivel, pois o tempo é negativo.

C*

Função do 2º Grau - Máximo e Mínimo

Toda expressão na forma y = ax² + bx + c ou f(x) = ax² + bx + c com a, b e c números reais, sendo a ≠ 0, é denominada função do 2º grau. A representação gráfica de uma função do 2º grau é dada através de uma parábola, que pode ter a concavidade voltada para cima ou para baixo.


Para determinarmos o ponto máximo e o ponto mínimo de uma função do 2º grau basta calcular o vértice da parábola utilizando as seguintes expressões matemáticas:


Exemplos

1 – Na função y = x² - 2x +1, temos que a = 1, b = -2 e c = 1. Podemos verificar que
a > 0, então a parábola possui concavidade voltada para cima possuindo ponto mínimo. Vamos calcular as coordenadas do vértice da parábola.



As coordenadas do vértice são (1, 0).

2 – Dada a função y = -x² -x + 3, temos que a = -1, b = -1 e c = 3. Temos a < 0, então a parábola possui concavidade voltada para baixo tendo um ponto máximo. Os vértices da parábola podem ser calculados da seguinte maneira:



As coordenadas do vértice são (0,5; 3,25).

C*

Função do 2º Grau - Calculando

Determinar a raiz de uma função é calcular os valores de x que satisfazem a equação do 2º grau ax² + bx + c = 0, que podem ser encontradas através do Teorema de Bháskara:


onde, Δ = b² - 4.a.c



Número de raízes reais da função do 2º grau

Dada a função f(x) = ax² + bx + c, existirão três casos a serem considerados para a obtenção do número de raízes. Isso dependerá do valor do discriminante Δ.


1º caso → Δ > 0: A função possui duas raízes reais e distintas, isto é, diferentes.


2º caso → Δ = 0: A função possui raízes reais e iguais. Nesse caso, dizemos que a função possui uma única raiz.


3º caso → Δ <0:>



Soma e produto das raízes

Seja a equação, ax² + bx + c = 0, temos que:

Se Δ ≥ 0, a soma das raízes dessa equação é dada por e o produto das raízes por . De fato, x’ e x’’ são as raízes da equação, por isso temos:



Exemplo 1:

Seja f(x) = x²-2x+1 , encontre as raizes dessa equação. ( Ou seja, quais valores de x nos fornece f(x)=0 ? )

f(x)=0
x²-2x+1 = 0 ( a=1 , b=-2 , c=1)

Δ = b²-4.a.c
Δ = (-2)² - 4.1.1
Δ = 4-4 = 0

x' = -b+√Δ / 2.a = -(-2) + √0 /2.1 = 2/2 = 1

x'' = -b-√Δ /2.a = -(-2) - √0 /2.1 = 2/2 = 1

Entao, só existe uma única raiz para essa equação que é x=1.


Exemplo 2:


Seja f(x) = -x²+3x-2 , encontre as raizes dessa equação. ( Ou seja, quais valores de x nos fornece f(x)=0 ? )

f(x)=0
-x²+3x-2 = 0 ( a=-1, b=+3 , c=-2 )

Δ = b²-4.a.c
Δ = (+3)² - 4.(-1).(-2)
Δ = 9 - 8 = 1

x' = -b+√Δ / 2.a = -(3) + √1 /2.(-1) = -2/-2 = 1

x'' = -b-√Δ /2.a = -(3) - √1 /2.(-1) = -4/-2 = 2

Entao, existem duas raízes para essa equação que é x=1 e x=2.


C*

Função do 2º Grau - concavidade

O gráfico de uma função de 2º grau será uma parábola de concavidade para baixo ou para cima.

No primeiro momento, para construir um gráfico de uma função de 2º grau qualquer, basta atribuir valores para x e encontrar valores correspondentes para a função. Portanto, formaremos pares ordenados, com eles iremos construir o gráfico, veja alguns exemplos:

Exemplo 1:

Dada a função f(x) = x² – 1. Essa função pode ser escrita da seguinte forma: y = x² – 1.
Atribuiremos qualquer val0r para x e substituindo na função encontraremos o valor de y, formando pares ordenados.

y = (-3)² – 1
y = 9 – 1
y = 8
(-3,8)

y = (-2)² – 1
y = 4 – 1
y = 3
(-2,3)

y = (-1)² – 1
y = 1 – 1
y = 0
(-1,0)

y = 0² – 1
y = -1
(0,-1)

y = 1² – 1
y = 1 – 1
y = 0
(1,0)

y = 2² – 1
y = 4 – 1
y = 3
(2,3)

y = 3² – 1
y = 9 – 1
y = 8
(3,8)

Distribuindo os pares ordenados no plano cartesiano montaremos o gráfico.

O gráfico desse exemplo tem a concavidade voltada para cima, podemos relacionar a concavidade com o valor do coeficiente a, quando a > 0 a concavidade sempre será voltada para cima.


Exemplo 2:

Dada a função f(x) = -x². Essa função pode ser escrita da seguinte forma: y = 5x². Atribuiremos qualquer valor para x e substituindo na função encontraremos o valor de y, formando pares ordenados.

y = -(-3)²
y = - 9
(-3,-9)

y = -(-2)²
y = - 4
(-2,-4)

y = -(-1)²
y = -1
(-1,-1)

y = -(0)²
y = 0
(0,0)

y = -(1)²
y = -1
(1,-1)

y = -(2)²
y = -4
(2,-4)

y = -(3)²
y = -9
(3,-9)

Distribuindo os pares ordenados no plano cartesiano montaremos o gráfico.



O gráfico do exemplo 2 tem a concavidade voltada para baixo, como já foi dito na conclusão do exemplo 1 que a concavidade está relacionada com o valor do coeficiente a, quando a < 0 a concavidade sempre será voltada para baixo.

C*

Função do 2º Grau

Toda função estabelecida pela lei de formação f(x) = ax² + bx + c, com a, b e c números reais e a ≠ 0, é denominada função do 2º grau.

A representação geométrica de uma função do 2º grau é dada por uma parábola, que de acordo com o sinal do coeficiente a pode ter concavidade voltada para cima ou para baixo.

As raízes de uma função do 2º grau são os pontos onde a parábola intercepta o eixo x. Dada a função f(x) = ax² + bx + c, se f(x) = 0, obtemos uma equação do 2º grau,
ax² + bx + c = 0, dependendo do valor do discriminante ∆(delta), podemos ter as seguintes situações gráficas:

∆ > 0, a equação possui duas raízes reais e diferentes. A parábola intercepta o eixo x em dois pontos distintos.


∆ = 0, a equação possui apenas uma raiz real. A parábola intercepta o eixo x em um único ponto.

∆ <0, a equação não possui raízes reais. A parábola não intercepta o eixo x.



C*

Complemento

UFBA - Considere a equação 10^{x + 0,4658} = 368. Sabendo-se que
log 3,68 = 0,5658 , calcule 10x.

Solução:
Temos: 10^{x + 0,4658} = 368
Daí, podemos escrever:
log 368 = x + 0,4658 \ x = log 368 - 0,4658
Ora, é dado que: log 3,68 = 0,5658, ou seja:
log(368/100) = 0,5658

Logo, log 368 - log 100 = 0,5658 \ log 368 - 2 = 0,5658 , já que
log 100 = 2 (pois 10² = 100).
Daí, vem então:
log 368 = 2,5658

Então, x = log 368 - 0,4658 = 2,5658 - 0,4658 = 2,1
Como o problema pede o valor de 10x, vem: 10.2,1 = 21
Resp: 21

Se log N = 2 + log 2 - log 3 - 2log 5 , calcule o valor de 30N.

Solução:
Podemos escrever:
logN = 2 + log2 - log3 - log5²
logN = 2 + log2 - log3 - log25
logN = 2 + log2 - (log3 + log25)
Como 2 = log100, fica:
logN = (log100 + log2) - (log3 + log25)
logN = log(100.2) - log(3.25)
logN = log200 - log75
logN = log(200/75)

Logo, concluímos que N = 200/75
Simplificando, fica:
N = 40/15 = 8/3
Logo, 30N = 30(8/3) = 80
Resp: 30N = 80

C*

Função polinomial

Toda função na forma P(x) = a_nxⁿ + a_n-1x^n-1 + ... + a₂x² + a₁x + a₀, é considerada uma função polinomial, onde p(x) está em função do valor de x. A cada valor atribuído a x existe um valor em y, pois x: domínio da função e y: imagem.

O grau de um polinômio é expresso através do maior expoente natural entre os monômios que o formam. Veja:

g(x) = 4x⁴ + 10x² – 5x + 2: polinômio grau 4.
f(x) = -9x⁶ + 12x³ - 23x² + 9x – 6: polinômio grau 6.
h(x) = -3x³ + 9x2 – 5x + 6: polinômio grau 3.

Em uma função polinomial, à medida que os valores de x são atribuídos descobrimos os respectivos valores em y [p(x)], construindo o par ordenado (x,y), usado nas representações gráficas no plano cartesiano. Observe:

Dada a função polinomial p(x) = 2x³ + 2x² – 5x + 1. Determine os pares ordenados quando:
x = 0
p(x) = 2x³ + 2x² – 5x + 1
p(0) = 2*0³ + 2*0² – 5*0 + 1
p(0) = 0 + 0 – 0 + 1
p(0) = 1
par ordenado (0,1)

x = 1
p(1) = 2*1³ + 2*1² – 5*1 + 1
p(1) = 2 + 2 – 5 + 1
p(1) = 0
par ordenado (1,0)

x = 2
p(2) = 2*2³ + 2*2² – 5*2 + 1
p(2) = 2*8 + 2*4 – 10 + 1
p(2) = 16 + 8 – 10 + 1
p(2) = 15
par ordenado (2,15)


Polinômio nulo

Dizemos que um polinômio é nulo quando todos os seus coeficientes forem iguais a zero. P(x) = 0.

Identidade entre polinômios

Dois polinômios são idênticos quando todos os seus coeficientes são números iguais. Observe:

ax² + (b+3)x +(c–7) ≡ –2x² + 6x – 9

Para que esses polinômios sejam idênticos os coeficientes de mesmo grau precisam ser iguais, então:
a = – 2
b + 3 = 6 b = 6 – 3 b = 3
c – 7 = – 9 c = – 9 + 7 c = – 2


(a+2)x³ + (b-26)x² + (c+6)x +(d-7) ≡ 2x³ + 5x² + 2x - 9

a+2 = 2 a = 2-2 a = 0
b-26 = 5 b = 5+26 b = 31
c+6 = 2 c = 2-6 c = -4
d-7 = - 9 d = -9+7 d = -2



C*

Função Par e Ímpar

Função Par

Estudaremos a forma pela qual se constitui a função f(x) = x² – 1, representada no gráfico cartesiano. Note que na função, temos:
f(1) = 0; f(–1) = 0 e f(2) = 3 e f(–2) = 3.

f(–1) = (–1)² – 1 = 1 – 1 = 0
f(1) = 1² – 1 = 1 – 1 = 0

f(–2) = (–2)² –1 = 4 – 1 = 3
f(2) = 2² – 1 = 4 – 1 = 3

Observe pelo gráfico que existe uma simetria em relação ao eixo y. As imagens dos domínios x = – 1 e x = 1 são correspondentes com y = 0 e os domínios x = –2 e x = 2 formam pares ordenados com a mesma imagem y = 3. Para valores simétricos do domínio, a imagem assume o mesmo valor. A esse tipo de ocorrência damos a classificação de função par.

Uma função f é considerada par quando f(–x) = f(x), qualquer que seja o valor de x Є D(f).

Função ímpar

Analisaremos a função f(x) = 2x, de acordo com o gráfico. Nessa função, temos que: f(–2) = – 4; f(2) = 4.

f(–2) = 2 * (–2) = – 4

f(2) = 2 * 2 = 4

Observe o gráfico e visualize que existe uma simetria em relação ao ponto das origens. No eixo das abcissas (x), temos os pontos simétricos (2;0) e (–2;0), e no eixo das ordenadas (y), temos os pontos simétricos (0;4) e (0;–4). Nessa situação, a função é classificada como ímpar.

Uma função f é considerada ímpar quando f(–x) = – f(x), qualquer que seja o valor de x Є D(f).

C*

Propriedades do Logaritmo

Para resolver um logaritmo, fazemos a seguinte conta:

Temos,
log_a b = x

portanto,

a^x = b

Exemplo

log₂ 8 = x
2^x = 8
x=3 ( resposta )


Propriedade do produto do logaritmo

Se encontrarmos um logaritmo do tipo: log_a(x * y) devemos resolvê-lo, somando o logaritmo de x na base a e o logaritmo de y na base a.

log_a (x * y) = log_a x + log_a y

Exemplo:

log₂(32 * 16) = log₂32 + log₂16 = 5 + 4 = 9


Propriedades do quociente do logaritmo

Caso o logaritmo seja do tipo log_ax/y, devemos resolvê-lo subtraindo o logaritmo do numerador na base a pelo logaritmo do denominador também na base a.

log_ax/y = log_ax – log_ay

Exemplo:
log₅(625/125) = log₅625 – log₅125 = 4 – 3 = 1


Propriedade da potência do logaritmo

Quando um logaritmo estiver elevado a um expoente, na próxima passagem esse expoente irá multiplicar o resultado desse logaritmo, veja como:

log_ax^m = m*log_ax

Exemplo:
log₃81² = 2*log₃81 = 2 * 4 = 8

C*

Função Logaritmica

Toda função definida pela lei de formação f(x) = log_ax, com a ≠ 1 e a > 0, é denominada função logarítmica de base a. Nesse tipo de função o domínio é representado pelo conjunto dos números reais maiores que zero e o contradomínio, o conjunto dos reais.

Exemplos de funções logarítmicas:

f(x) = log₂x
f(x) = log₃x
f(x) = log_1/2x
f(x) = log₁₀x
f(x) = log_1/3x
f(x) = log₄x
f(x) = log₂(x – 1)
f(x) = log_0,5x


Determinando o domínio da função logarítmica

Dada a função f(x) = _{(x – 2)}(4 – x), temos as seguintes restrições:

1) 4 – x > 0 → – x > – 4 → x <> 0 → x > 2
3) x – 2 ≠ 1 → x ≠ 1+2 → x ≠ 3

Realizando a intersecção das restrições 1, 2 e 3, temos o seguinte resultado: 2 <>.

Dessa forma, D = {x Є R / 2
Gráfico de uma função logarítmica

Para a construção do gráfico da função logarítmica devemos estar atentos a duas situações:

a > 1

0 1


Para a > 1, temos o gráfico da seguinte forma:

Função crescente

Para 0 <>

Função decrescente


C*

Função Inversa

Para voce definir uma função inversa, basta transformar o que é domínio na função f na imagem na f -1 e vice e versa.

Dada uma sentença de uma função y = f(x), para encontrar a sua inversa é preciso seguir alguns passos.

Dada a função y = 3x – 5 determinaremos a sua inversa da seguinte maneira:

1º passo: isolar x.
y = 3x – 5
y + 5 = 3x
x = (y + 5)/3

2º passo: troca-se x por y e y por x, pois é mais usual termos como variável independente a letra x.

y = (x + 5)/3


Portanto, a função f(x) = 3x – 5 terá inversa igual a f –1 (x) = (x + 5)/3


Exemplo

Dada a função f(x) = x² a sua inversa será:

Isolando x:
y = x²
√y = x

Invertendo x por y e y por x:
y = √x

Portanto, f –1(x) = √x

C*

função exponencial

Toda relação de dependência, onde uma incógnita depende do valor da outra, é denominada função. A função denominada como exponencial possui essa relação de dependência e sua principal característica é que a parte variável representada por x se encontra no expoente. Observe:

y = 2 ^x
y = 3 ^{x + 4}
y = 0,5 ^x
y = 4 ^x

A lei de formação de uma função exponencial indica que a base elevada ao expoente x precisa ser maior que zero e diferente de um, conforme a seguinte notação:

f: R→R tal que y = a ^x, sendo que a > 0 e a ≠ 1.

Uma função pode ser representada através de um gráfico, e no caso da exponencial, temos duas situações: a > 0 e 0 <>

Exemplo 1

(Unit-SE) Uma determinada máquina industrial se deprecia de tal forma que seu valor, t anos após a sua compra, é dado por v(t) = v₀ * 2 ^–0,2t, em que v₀ é uma constante real. Se, após 10 anos, a máquina estiver valendo R$ 12 000,00, determine o valor que ela foi comprada.
Temos que v(10) = 12 000, então:

v(10) = v0 * 2 ^–0,2*10

12 000 = v0 * 2 ^–2

12 000 = v0 * 1/4

12 000 : 1/ 4 = v0

v0 = 12 000 * 4

v0 = 48 000

A máquina foi comprada pelo valor de R$ 48 000,00.

Exercicio:

(EU-PI) Suponha que, em 2003, o PIB (Produto Interno Bruto) de um país seja de 500 bilhões de dólares. Se o PIB crescer 3% ao ano, de forma cumulativa, qual será o PIB do país em 2023, dado em bilhões de dólares? Use 1,03²⁰ = 1,80.

resp: 900 bilhões de dólares.

C*

Função Composta

A função composta pode ser entendida pela determinação de uma terceira função C, formada pela junção das funções A e B. Matematicamente falando, temos que f: A → B e g: B → C, denomina a formação da função composta de g com f, h: A → C. Dizemos função g composta com a função f, representada por gof.

Exemplo 1

Ao considerarmos as funções f(x) = 4x e g(x) = x² + 5, determinaremos:

a) g o f

(g o f)(x) = g(f(x))

g(x) = x² + 5
g(4x) = (4x)² + 5
g(4x) = 16x² + 5

(g o f)(x) = g(f(x)) = 16x² + 5



b) f o g

(f o g)(x) = f(g(x))

f(x) = 4x
f(x² + 5) = 4 * (x² + 5)
f(x² + 5) = 4x² + 20

(f o g)(x) = f(g(x)) = 4x² + 20


exercícios: (Usando as mesmas funções do exemplo 1 )

a) (g o f)(x) = g(f(x))
resp: 4x² + 16x + 15

b) (f o g)(x) = f(g(x))
resp: 4x² + 1



C*

Função Simples

Uma relação estabelecida entre dois conjuntos A e B, onde exista uma associação entre cada elemento de A com um único de B através de uma lei de formação é considerada uma função. Observe o exemplo:

Obs: Para cada valor dos elementos de A ( Dominio) só pode ter um valor de B (Imagem)

Um exemplo de relação de função pode ser expresso por uma lei de formação que relaciona: o preço a ser pago em função da quantidade de litros de combustível abastecidos. Considerando o preço da gasolina igual a R$ 2,50, temos a seguinte lei de formação: f(x) = 2,50*x, onde f(x): preço a pagar e x: quantidade de litros. Observe a tabela abaixo:

Verifique que para cada valor de x temos uma representação em f(x), esse modelo é um típico exemplo de função do 1º grau.

C*

Conjuntos

Conjunto vazio: é um conjunto que não possui elementos. O conjunto vazio é representado por { } ou .

---

Subconjuntos: quando todos os elementos de um conjunto A qualquer pertencem a um outro conjunto B, diz-se, então, que A é um subconjunto de B, ou seja AB. Observações:

• Todo o conjunto A é subconjunto dele próprio, ou seja ;
• O conjunto vazio, por convenção, é subconjunto de qualquer conjunto, ou seja

  ---

União de Conjuntos: dados os conjuntos A e B, define-se como união dos conjuntos A e B ao conjunto representado por , formado por todos os elementos pertencentes a A ou B, ou seja:



---

Intersecção de Conjuntos: dados os conjuntos A e B, define-se como intersecção dos conjuntos A e B ao conjunto representado por , formado por todos os elementos pertencentes a A e B, simultaneamente, ou seja:



---

Diferença de Conjuntos: dados os conjuntos A e B, define-se como diferença entre A e B (nesta ordem) ao conjunto representado por A-B, formado por todos os elementos pertencentes a A, mas que não pertencem a B, ou seja



---

Produto Cartesiano: dados os conjuntos A e B, chama-se peoduto cartesiano A com B, ao conjunto AxB, formado por todos os pares ordenados (x,y), onde x é elemento de A e y é elemento de B, ou seja

Número de subconjuntos de um conjunto: se um conjunto A possuir n elementos, então existirão 2ⁿ subconjuntos de A.




C*