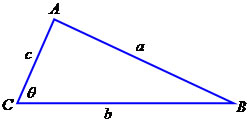
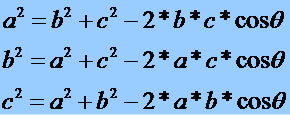A fecundação ocorrerá ao acaso, pois não sabemos qual espermatozoide, A ou a será responsável pela concepção ou qual célula feminina será fecundada A ou a.
Observe o esquema:
Veja o quadro de possibilidades: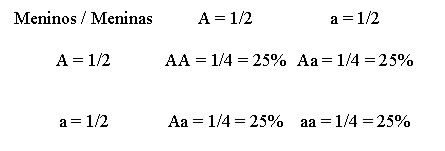
Exemplo
Um homem e uma mulher possuem pigmentação normal. O homem é filho de um pai normal e uma mãe albina. A mulher é filha de uma mãe normal e um pai albino. Determine a probabilidade deles terem um filho albino do sexo masculino.
Homem = Aa
Mulher = Aa
Probabilidade de criança albina = 1/4
Probabilidade de criança sexo masculino = 1/4 + 1/4 = 2/4 = 1/2
Os eventos criança albina e criança sexo masculino são independentes, dessa forma temos que para a criança ser albina e possuir o sexo masculino a probabilidade é a seguinte: 1/2 * 1/4 = 1/8 ou 12,5%.
C*






 .
. o valor de 0,529.
o valor de 0,529. . Essa experiência foi realizada por Kerrich e Buffon.
. Essa experiência foi realizada por Kerrich e Buffon.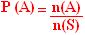
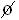 ) = 0
) = 0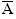 ) =1
) =1