Função Par e Ímpar

Função Par

Estudaremos a forma pela qual se constitui a função f(x) = x² – 1, representada no gráfico cartesiano. Note que na função, temos:
f(1) = 0; f(–1) = 0 e f(2) = 3 e f(–2) = 3.

f(–1) = (–1)² – 1 = 1 – 1 = 0
f(1) = 1² – 1 = 1 – 1 = 0

f(–2) = (–2)² –1 = 4 – 1 = 3
f(2) = 2² – 1 = 4 – 1 = 3

Observe pelo gráfico que existe uma simetria em relação ao eixo y. As imagens dos domínios x = – 1 e x = 1 são correspondentes com y = 0 e os domínios x = –2 e x = 2 formam pares ordenados com a mesma imagem y = 3. Para valores simétricos do domínio, a imagem assume o mesmo valor. A esse tipo de ocorrência damos a classificação de função par.

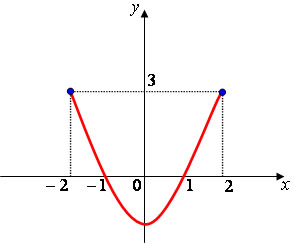
Uma função f é considerada par quando f(–x) = f(x), qualquer que seja o valor de x Є D(f).

Função ímpar

Analisaremos a função f(x) = 2x, de acordo com o gráfico. Nessa função, temos que: f(–2) = – 4; f(2) = 4.

f(–2) = 2 * (–2) = – 4

f(2) = 2 * 2 = 4

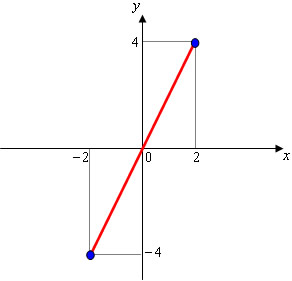
Observe o gráfico e visualize que existe uma simetria em relação ao ponto das origens. No eixo das abcissas (x), temos os pontos simétricos (2;0) e (–2;0), e no eixo das ordenadas (y), temos os pontos simétricos (0;4) e (0;–4). Nessa situação, a função é classificada como ímpar.

Uma função f é considerada ímpar quando f(–x) = – f(x), qualquer que seja o valor de x Є D(f).

C*