NO FERIADO DO DIA 12/10 VIRÃO NOVAS ATUALIZAÇÕES !

Probabilidade na genética

Vamos supor que um indivíduo heterozigoto para determinada característica (Aa) forma dois tipos de espermatozoides, A e a. Caso uma mulher também seja heterozigota, formará óvulos A e a.

A fecundação ocorrerá ao acaso, pois não sabemos qual espermatozoide, A ou a será responsável pela concepção ou qual célula feminina será fecundada A ou a.

Observe o esquema:

Veja o quadro de possibilidades: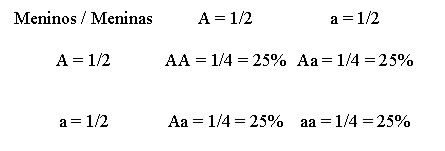

Exemplo

Um homem e uma mulher possuem pigmentação normal. O homem é filho de um pai normal e uma mãe albina. A mulher é filha de uma mãe normal e um pai albino. Determine a probabilidade deles terem um filho albino do sexo masculino.

Homem = Aa
Mulher = Aa

Probabilidade de criança albina = 1/4
Probabilidade de criança sexo masculino = 1/4 + 1/4 = 2/4 = 1/2

Os eventos criança albina e criança sexo masculino são independentes, dessa forma temos que para a criança ser albina e possuir o sexo masculino a probabilidade é a seguinte: 1/2 * 1/4 = 1/8 ou 12,5%.

C*

União de eventos

Dados dois eventos A e B de um espaço amostral S a probabilidade de ocorrer A ou B é dada por:

P(A U B) = P(A) + P(B) – P(A ∩ B)



Verificação:

O Número de elementos de A U B é igual à soma do número de elementos de A com o número de elementos de B, menos uma vez o número de elementos de A ∩ B que foi contado duas vezes (uma em A e outra em B). Assim temos:

n(AUB) = n(A) + n(B) – n(A∩B)
Dividindo por n(S) [S ≠ ] resulta



P(AUB) = P(A) + P(B) – P(A∩B)

Exemplo:

Numa urna existem 10 bolas numeradas de 1 a 10. Retirando uma bola ao acaso, qual a probabilidade de ocorrer múltiplos de 2 ou múltiplos de 3?



A é o evento “múltiplo de 2”.
B é o evento “múltiplo de 3”.

P(AUB) = P(A) + P(B) – P(A∩B) =

C*

Exemplo

Clique na imagem para ampliá-la.

Probabilidade Condicional

Probabilidade condicional é um segundo evento de um espaço amostral que ocorre em um evento depois que já tenha ocorrido o primeiro.

Para melhor compreensão do que seja probabilidade condicional, considere um espaço amostral S finito não vazio e um evento A de S, se quisermos outro evento B desse espaço amostral S, essa nova probabilidade é indicada por P(B | A) e dizemos que é a probabilidade condicional de B em relação a A.

Essa probabilidade condicional irá formar um novo espaço amostral, pois agora o espaço amostral será A e os elementos do evento B irão pertencer a B ∩ A.



Para calcular a probabilidade P(B | A) deve-se seguir o mesmo raciocínio da fórmula , portanto

P(B | A) = n(B ∩ A) ou P(B | A) = P(B ∩ A)
n(A) P(A)

E para calcular a probabilidade P(B∩A) basta multiplicar as probabilidades de A e B:

P(B∩A) = P(A) . P(B)

Exemplos

1- Um casal possui 2 filhos. Qual a probabilidade de ambos serem do sexo masculino?

Os eventos {nascer uma criança do sexo masculino} e {nescer uma criança do sexo feminino} são equiprováveis. Logo, a probabilidade de nascer um filho do sexo masculino é 1/2. A ocorrência do evento {o primeiro filho é do sexo masculino} não influencia a ocorrência do evento {o segundo filho é do sexo masculino}, e então:

2 - Uma urna contém 10 bolas brancas, 5 bolas amarelas e 10 bolas pretas. Uma bola é
escolhida ao acaso da urna e verifica-se que não é preta, qual a probabilidade de ser amarela?

A = a bola selecionada é amarela
B = a bola selecionada é preta

P(A|Bc) = P(A \ Bc).P(Bc) = P(A).P(Bc) = 5/25 . 15/25 = 1/3

Sendo Bc o evento B complementar, ou seja, bola não preta.


C*

Espaço Amostral

Consideremos uma experiência onde pode ocorrer n resultados possíveis. Cada um dos n resultados possíveis será chamado ponto amostral, e o conjunto S de todos os resultados possíveis, ou seja, o conjunto S de todos os pontos amostrais será chamado espaço amostral da experiência.


Cada bola representa um resultado possivel.


Exemplo:
► Lançamento de uma moeda:
Existem dois resultados possíveis, portanto S = {“cara”, “coroa”}



► Lançamento de um dado:
Existe 6 resultados possíveis, portanto S = { 1, 2, 3, 4, 5, 6}




Evento

Chama-se evento qualquer subconjunto A do espaço amostral S.

A está contido em S

Exemplo:

► No lançamento de um dado, o evento “número ímpar” é A = { 1; 3; 5}
► Na experiência “retirar uma bola de uma urna” que contém três bolas brancas (b₁, b₂, b₃), e duas bolas pretas (p₁, p₂), o espaço amostral é:
S = {b₁, b₂, b₃, p₁, p₂}, onde o evento “bola branca” é: {b₁, b₂, b₃}

Evento Impossível e Evento Certo

O conjunto vazio também é um subconjunto de S ( está contido em S), portanto, também é um evento; é chamado evento impossível, pois nunca ocorre.
O conjunto S é subconjunto de si próprio, portanto S também é um evento; S é chamado de evento certo, pois sempre acontece.

Evento Complementar

Chama-se de evento complementar de um evento A num espaço amostral S, ao evento tal que = S – A.

está de verde.

Notemos que A ∩ C = e A U = S

Exemplo:

No lançamento de um dado, o evento complementar do evento “número ímpar” é o evento “número par”
A = { 1, 3, 5}
= {2, 4, 6}

C*

Probabilidade

Consideremos a experiência do lançamento de uma moeda e leitura da face voltada para cima. Ao realizarmos n vezes a experiência, se obtivermos m vezes o resultado “cara” é . É claro que lançada a moeda o resultado é imprevisível, pois não podemos dizer com absoluta certeza que o resultado será “cara”, pois nada impede que dê “coroa”.

A Experiência provou que conforme se aumenta n, ou seja, à medida que mais lançamentos da moeda são feitos, a freqüência relativa tende a estabilizar-se em torno de .

Exemplo:

Em 1000 lançamentos (n = 1000), 529 resultados foram favoráveis (m = 529), o que nos dá para o valor de 0,529.
Em 4040 lançamentos, 2048 resultados foram favoráveis o que nos da = 0,50693, isso significa que no lançamento de uma moeda “honesta” a probabilidade de se obter “cara” é . Essa experiência foi realizada por Kerrich e Buffon.

A definição que permite calcular teoricamente a probabilidade de um evento, sem realizar a experiência é:

Dado um espaço amostral S, com n (S) elementos, e um evento a de S, com n(A) elementos, a probabilidade do evento A é o P(A) tal que:

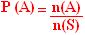
Propriedades

Sendo S ≠ um espaço amostral qualquer, A um evento de S e o complementar de A em S, valem as seguintes propriedades:

► P( 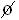) = 0
► P(S) = 1
► 0 ≤ P(A) ≤ 1

► P(A) + P( 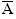) =1

C*

Lei do Seno

Fórmula que representa a lei dos senos:

Na lei dos senos utilizamos relações envolvendo o seno do ângulo e a medida oposta ao ângulo.

Exemplo 1

Determine o valor de x no triângulo a seguir.

sen120º = sen(180º – 120º) = sen60º = √3/2 ou 0,865
sen45º = √2/2 ou 0,705

Exemplo 2

No triângulo a seguir temos dois ângulos, um medindo 45º, outro medindo 105º, e um dos lados medindo 90 metros. Com base nesses valores determine a medida de x.

Para determinarmos a medida de x no triângulo devemos utilizar a lei dos senos, mas para isso precisamos descobrir o valor do terceiro ângulo do triângulo. Para tal cálculo utilizamos a seguinte definição: a soma dos ângulos internos de um triângulo é igual a 180º. Portanto:

α + 105º + 45º = 180º
α + 150º = 180º
α = 180º – 150º
α = 30º

Aplicando a lei dos senos




C*

lei do cosseno

Utilizamos a lei dos cossenos nas situações envolvendo triângulos não retângulos, isto é, triângulos quaisquer. Esses triângulos não possuem ângulo reto, portanto as relações trigonométricas do seno, cosseno e tangente não são válidas. Para determinarmos valores de medidas de ângulos e medidas de lados utilizamos a lei dos cossenos, que é expressa pela seguinte lei de formação:

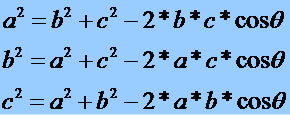
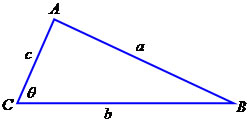
Exemplo 1

Utilizando a lei dos cossenos, determine o valor do segmento x no triângulo a seguir:

a² = b² + c² – 2 * b * c * cosӨ
7² = x² + 3² – 2 * 3 * x * cos60º
49 = x² + 9 – 6 * x * 0,5
49 = x² + 9 – 3x
x² –3x – 40 = 0

Aplicando o método resolutivo da equação do 2º grau, temos:

x’ = 8 e x” = – 5, por se tratar de medidas descartamos x” = –5 e utilizamos x’ = 8. Então o valor de x no triângulo é 8 cm.

Exemplo 2

Em um triângulo ABC, temos as seguintes medidas: AB = 6 cm, AC = 5 cm e BC = 7 cm. Determine a medida do ângulo A.

Vamos construir o triângulo com as medidas fornecidas no exercício.

Aplicando a lei dos cossenos

a = 7, b = 6 e c = 5

7² = 6² + 5² – 2 * 6 * 5 * cos A
49 = 36 + 25 – 60 * cos A
49 – 36 – 25 = –60 * cos A
–12 = –60 * cos A
12 = 60 * cos A
12/60 = cos A
cos A = 0,2

O ângulo que possui cosseno com valor aproximado de 0,2 mede 78º.


Exemplo 3

Calcule a medida da maior diagonal do paralelogramo da figura a seguir, utilizando a lei dos cossenos.

cos 120º = –cos(180º – 120º) = – cos 60º = – 0,5

x² = 5² + 10² – 2 * 5 * 10 * cos 60º
x² = 25 + 100 – 100 * (–0,5)
x² = 125 + 50
x² = 175
√x² = √175
x = √5² * 7
x = 5√7


C*