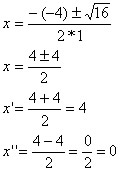Inequação do 2º grau

As inequações são expressões matemáticas que utilizam na sua formatação, os seguintes sinais de desigualdades:

>: maior que
<: br="" menor="" que="">≥: maior ou igual
≤: menor ou igual
≠: diferente


As inequações do 2º grau são resolvidas utilizando o teorema de Bháskara. O resultado deve ser comparado ao sinal da inequação, com o objetivo de formular o conjunto solução.

Exemplo 1

Vamos resolver a inequação 3x² + 10x + 7 < 0.

S = {x Є R / –7/3 < x < –1}

Exemplo 2

Determine a solução da inequação –2x² – x + 1 ≤ 0.

S = {x Є R / x < –1 ou x > 1/2}



Exemplo 3

Determine a solução da inequação x² – 4x ≥ 0.

S = {x Є R / x ≤ 0 ou x ≥ 4}

Exemplo 4

Calcule a solução da inequação x² – 6x + 9 > 0.

S = {x Є R / x < 3 e x > 3}

OBS: SEMPRE coloquem a solução do jeito mostrado.

c*

NO FERIADO DO DIA 12/10 VIRÃO NOVAS ATUALIZAÇÕES !

Probabilidade na genética

Vamos supor que um indivíduo heterozigoto para determinada característica (Aa) forma dois tipos de espermatozoides, A e a. Caso uma mulher também seja heterozigota, formará óvulos A e a.

A fecundação ocorrerá ao acaso, pois não sabemos qual espermatozoide, A ou a será responsável pela concepção ou qual célula feminina será fecundada A ou a.

Observe o esquema:

Veja o quadro de possibilidades:

Exemplo

Um homem e uma mulher possuem pigmentação normal. O homem é filho de um pai normal e uma mãe albina. A mulher é filha de uma mãe normal e um pai albino. Determine a probabilidade deles terem um filho albino do sexo masculino.

Homem = Aa
Mulher = Aa

Probabilidade de criança albina = 1/4
Probabilidade de criança sexo masculino = 1/4 + 1/4 = 2/4 = 1/2

Os eventos criança albina e criança sexo masculino são independentes, dessa forma temos que para a criança ser albina e possuir o sexo masculino a probabilidade é a seguinte: 1/2 * 1/4 = 1/8 ou 12,5%.

C*

União de eventos

Dados dois eventos A e B de um espaço amostral S a probabilidade de ocorrer A ou B é dada por:

P(A U B) = P(A) + P(B) – P(A ∩ B)



Verificação:

O Número de elementos de A U B é igual à soma do número de elementos de A com o número de elementos de B, menos uma vez o número de elementos de A ∩ B que foi contado duas vezes (uma em A e outra em B). Assim temos:

n(AUB) = n(A) + n(B) – n(A∩B)
Dividindo por n(S) [S ≠ ] resulta



P(AUB) = P(A) + P(B) – P(A∩B)

Exemplo:

Numa urna existem 10 bolas numeradas de 1 a 10. Retirando uma bola ao acaso, qual a probabilidade de ocorrer múltiplos de 2 ou múltiplos de 3?



A é o evento “múltiplo de 2”.
B é o evento “múltiplo de 3”.

P(AUB) = P(A) + P(B) – P(A∩B) =

C*

Exemplo

Clique na imagem para ampliá-la.

Probabilidade Condicional

Probabilidade condicional é um segundo evento de um espaço amostral que ocorre em um evento depois que já tenha ocorrido o primeiro.

Para melhor compreensão do que seja probabilidade condicional, considere um espaço amostral S finito não vazio e um evento A de S, se quisermos outro evento B desse espaço amostral S, essa nova probabilidade é indicada por P(B | A) e dizemos que é a probabilidade condicional de B em relação a A.

Essa probabilidade condicional irá formar um novo espaço amostral, pois agora o espaço amostral será A e os elementos do evento B irão pertencer a B ∩ A.



Para calcular a probabilidade P(B | A) deve-se seguir o mesmo raciocínio da fórmula , portanto

P(B | A) = n(B ∩ A) ou P(B | A) = P(B ∩ A)
n(A) P(A)

E para calcular a probabilidade P(B∩A) basta multiplicar as probabilidades de A e B:

P(B∩A) = P(A) . P(B)

Exemplos

1- Um casal possui 2 filhos. Qual a probabilidade de ambos serem do sexo masculino?

Os eventos {nascer uma criança do sexo masculino} e {nescer uma criança do sexo feminino} são equiprováveis. Logo, a probabilidade de nascer um filho do sexo masculino é 1/2. A ocorrência do evento {o primeiro filho é do sexo masculino} não influencia a ocorrência do evento {o segundo filho é do sexo masculino}, e então:

2 - Uma urna contém 10 bolas brancas, 5 bolas amarelas e 10 bolas pretas. Uma bola é
escolhida ao acaso da urna e verifica-se que não é preta, qual a probabilidade de ser amarela?

A = a bola selecionada é amarela
B = a bola selecionada é preta

P(A|Bc) = P(A \ Bc).P(Bc) = P(A).P(Bc) = 5/25 . 15/25 = 1/3

Sendo Bc o evento B complementar, ou seja, bola não preta.


C*

Espaço Amostral

Consideremos uma experiência onde pode ocorrer n resultados possíveis. Cada um dos n resultados possíveis será chamado ponto amostral, e o conjunto S de todos os resultados possíveis, ou seja, o conjunto S de todos os pontos amostrais será chamado espaço amostral da experiência.


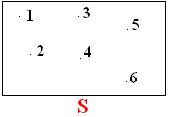
Cada bola representa um resultado possivel.


Exemplo:
► Lançamento de uma moeda:
Existem dois resultados possíveis, portanto S = {“cara”, “coroa”}



► Lançamento de um dado:
Existe 6 resultados possíveis, portanto S = { 1, 2, 3, 4, 5, 6}




Evento

Chama-se evento qualquer subconjunto A do espaço amostral S.

A está contido em S

Exemplo:

► No lançamento de um dado, o evento “número ímpar” é A = { 1; 3; 5}
► Na experiência “retirar uma bola de uma urna” que contém três bolas brancas (b₁, b₂, b₃), e duas bolas pretas (p₁, p₂), o espaço amostral é:
S = {b₁, b₂, b₃, p₁, p₂}, onde o evento “bola branca” é: {b₁, b₂, b₃}

Evento Impossível e Evento Certo

O conjunto vazio também é um subconjunto de S ( 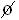está contido em S), portanto, 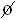também é um evento; 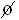é chamado evento impossível, pois nunca ocorre.
O conjunto S é subconjunto de si próprio, portanto S também é um evento; S é chamado de evento certo, pois sempre acontece.

Evento Complementar

Chama-se de evento complementar de um evento A num espaço amostral S, ao evento 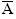tal que 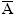= S – A.

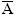está de verde.

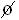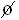Notemos que A ∩ C = e A U = S

Exemplo:

No lançamento de um dado, o evento complementar do evento “número ímpar” é o evento “número par”
A = { 1, 3, 5}
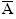= {2, 4, 6}

C*